Casual/Personal

Analysing 'Choose your own adventure' books

Casper

Nov 29, 2019 • 4 min read

A recent interest of mine has become analysing Choose your own adventure books. I've never read the original choose your own adventure books, but got introduced to it because of an upcoming project.

There are quite a few interesting things to observe in these books without even going into the actual stories. For several of the books I created a directed-graph of all the pages and choices.

Choose your own adventure - 2 - Journey Under the Sea

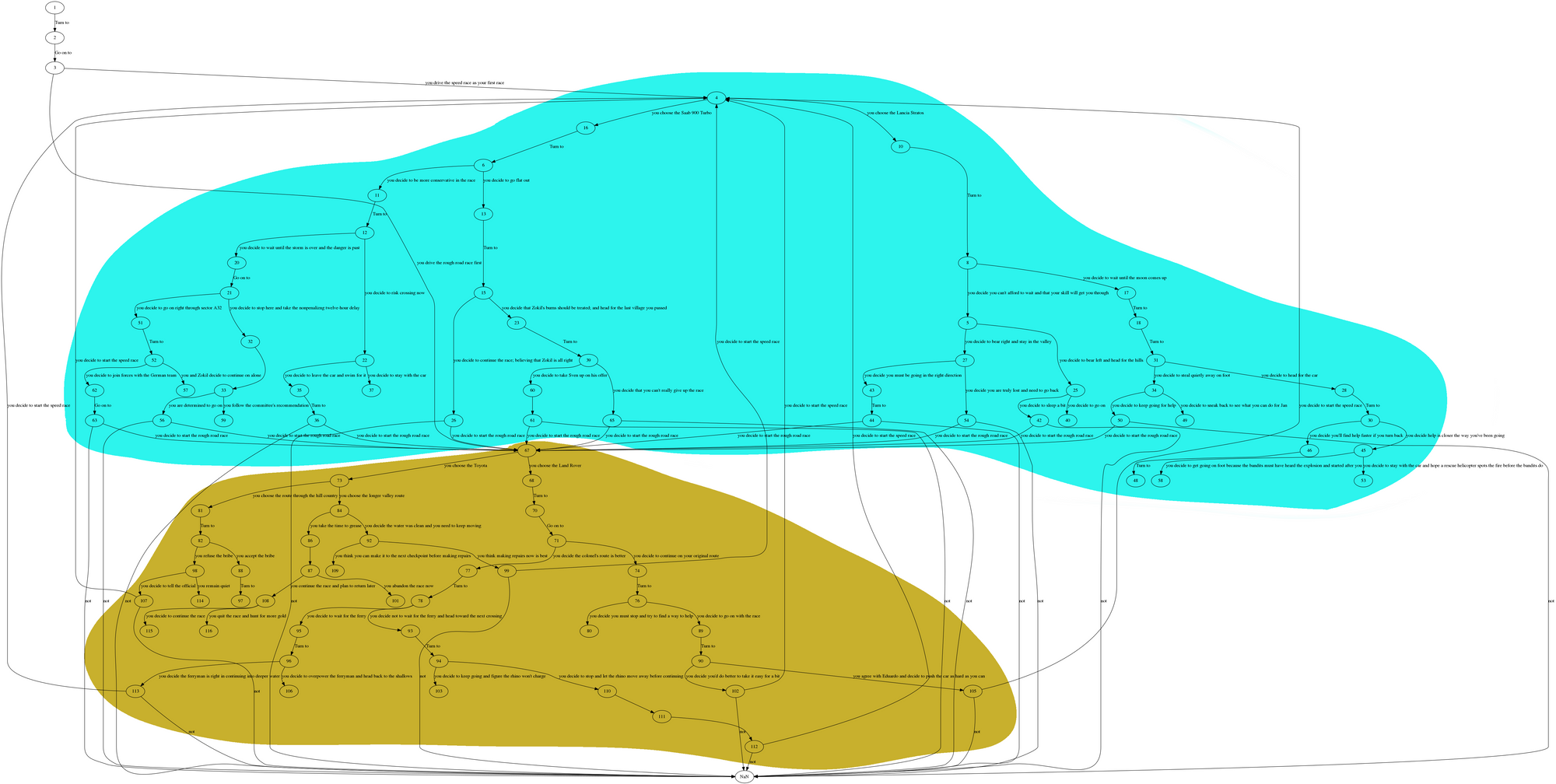
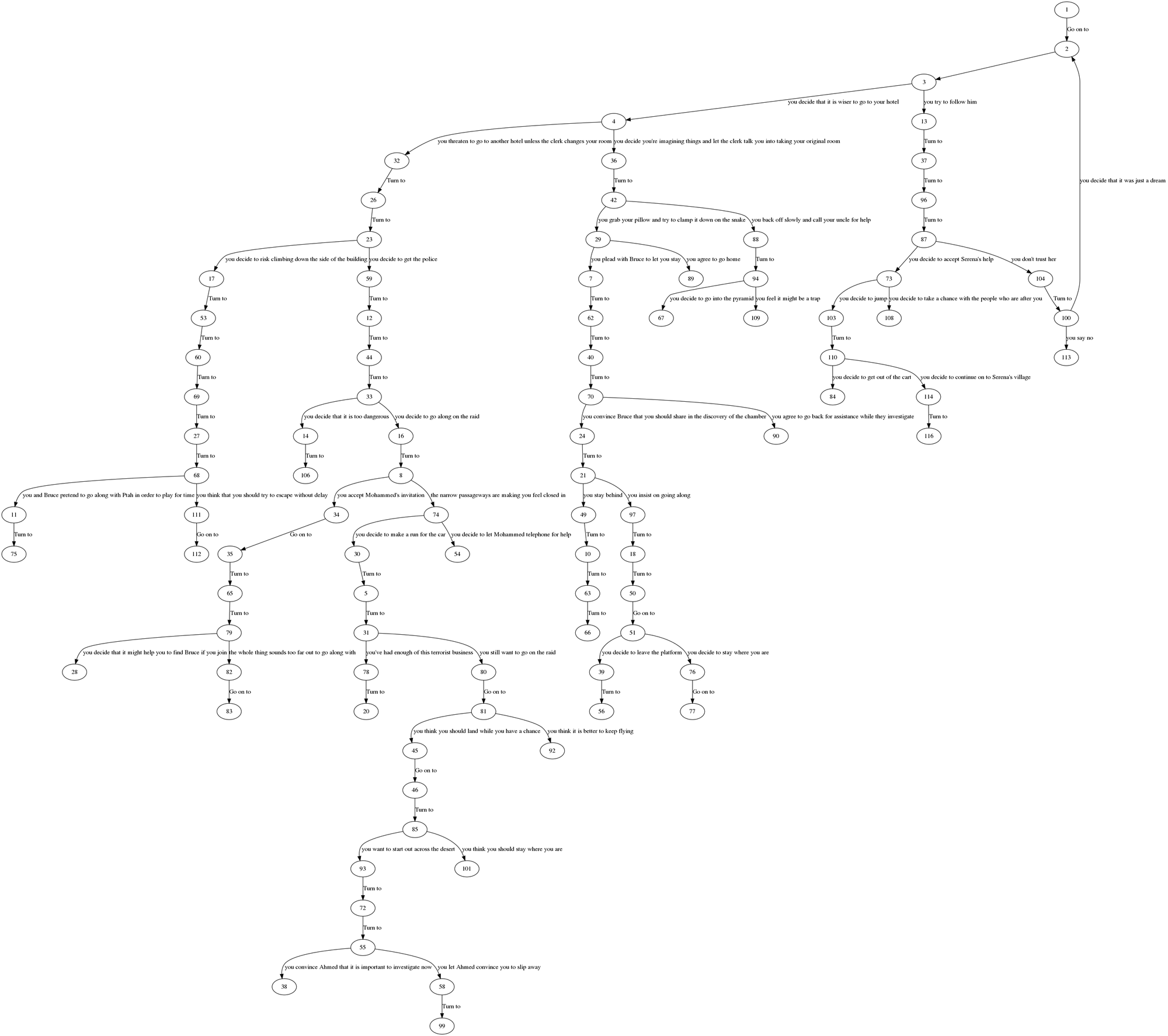
CYOA-2 is probably my favourite of all the books, it is complex and seems the most well-thought out. It must have taken a while to create it so that the story stays believable in all branches.

One strange part about this book is that page 111 is an ending, but it is unreachable, there is no way to get to it.
Page 110 is an ending as well, so there should have been a choice which gets you there. I'm not sure why this is, maybe a misprint, or maybe an error on my part. If you have any thoughts on this feel free to contact me.

Where a lot of the later books have a very deep tree structure, CYOA-2 is quite shallow, most choices can result in a unique ending.

There are some loops but you are unlikely to get to them, as only 2 pages the start of a cycle, page 9 and page 6. Funnily enough you can actually have to go through both of them to get a cycle in this book.

Summary:

CYOA-2:
- Possible Loops: 10		# Paths which result in a loop
- Edges: 108
- Total pages: 117		# Numbered pages in the book
- Reachable pages: 100
 - Endings: 41
 - Choice pages: 46		# Pages with 2 or more choices
 - Non-choice,Non-End: 13 	# Pages with no choice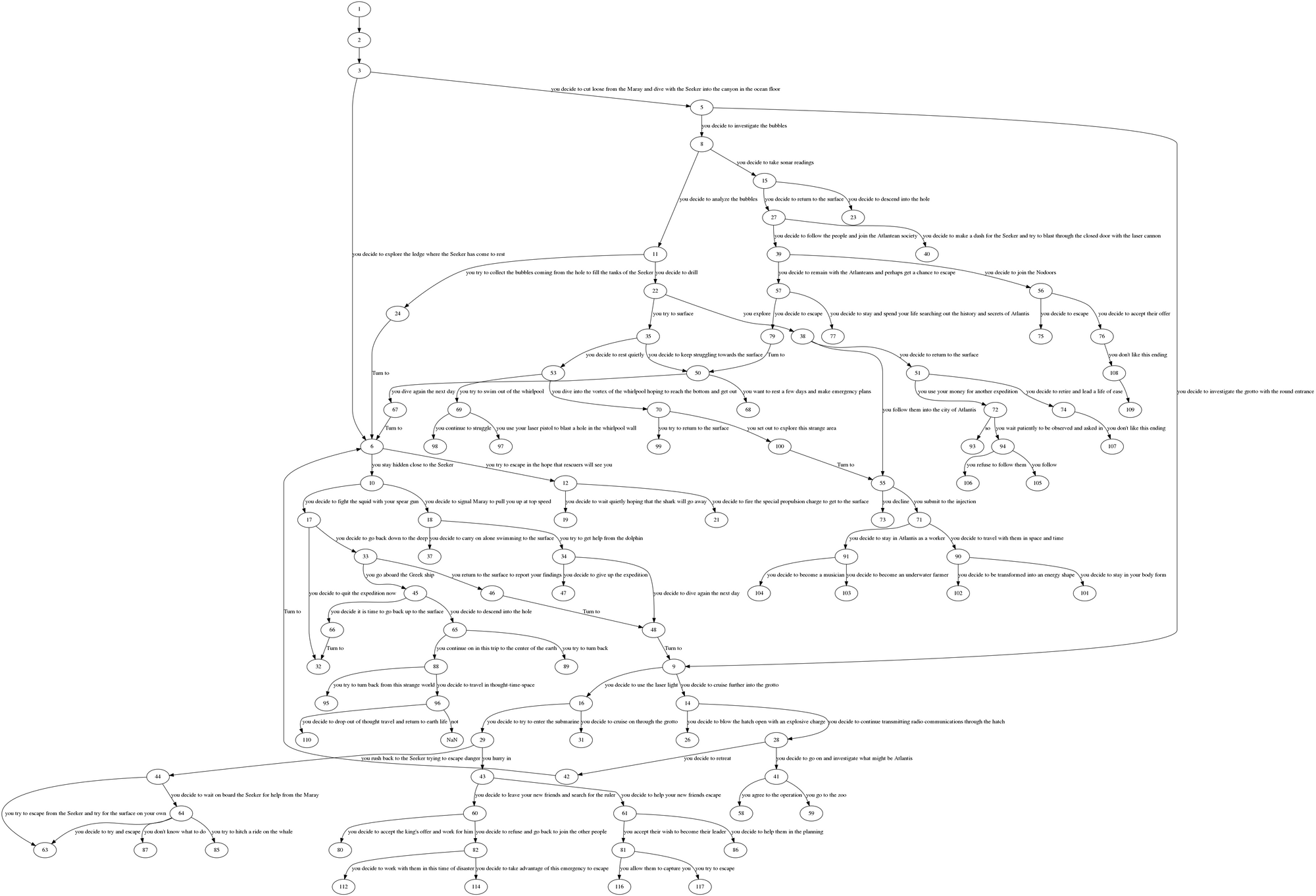

CYOA-2: The entire directed graph with the choices

Choose your own adventure - 17 - The Race Forever

CYOA-17 is the second book I mapped, the interesting thing about this book is that it is intended to be infinite as the title suggests. That's why there are 3 high-traffic nodes.

Page 4, The speed race
Page 67, The rough race
Page NaN, indicating an optional ending

To clarify, NaN would be 'The End' in something like:
If you decide to start the rough road race, turn to page 67. If not, The End.

One interesting thing in this book is that there is a clear divide between the speed race (marked in blue) and the rough race (marked in brown). Both branches are about the same size (in pages), even though blue looks bigger in this graph.

Summary:

CYOA-17:
- Possible Loops: 120
- Edges: 126
- Total pages: 116
- Reachable pages: 96
 - Endings: 33
 - Choice pages: 49
 - Non-choice,Non-End: 30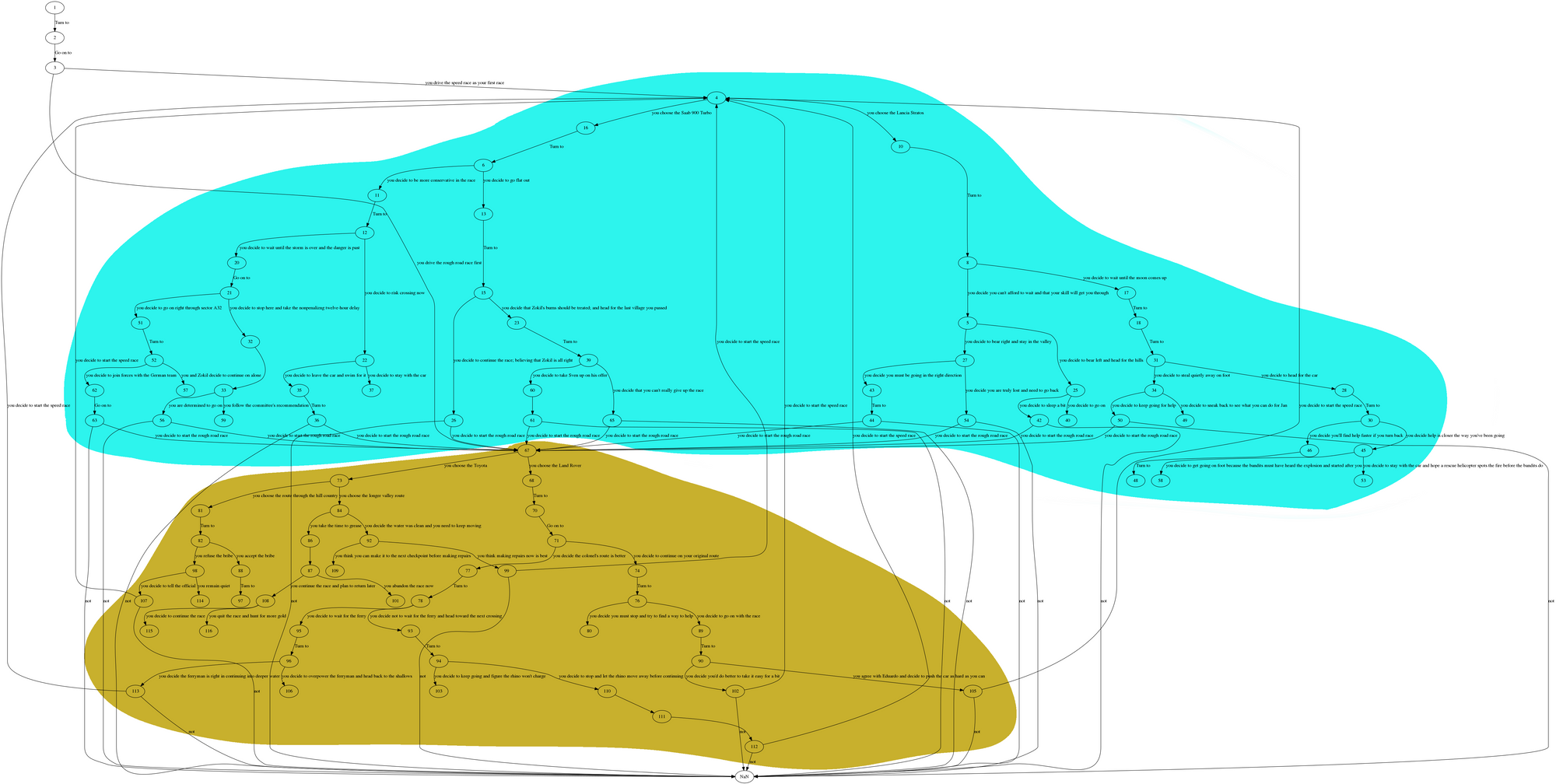

CYOA-17, with the 2 main branches marked

Choose your own adventure - 18 - Underground Kingdom

In contrast the CYOA-{2,17} this book has a pretty simple structure. There is a single cycle, which is only 2 edges long. And there are very little combining of branches going on, to the point at which you could almost make it an actual tree structure.

The main difference between this and CYOA-2 is that it has very few choices throughout the story. A lot of pages just go to the next page compared to earlier books.

I personally found this structure pretty boring, but it is good to have some variation compared to the more messy structures of CYOA-{2,17}.

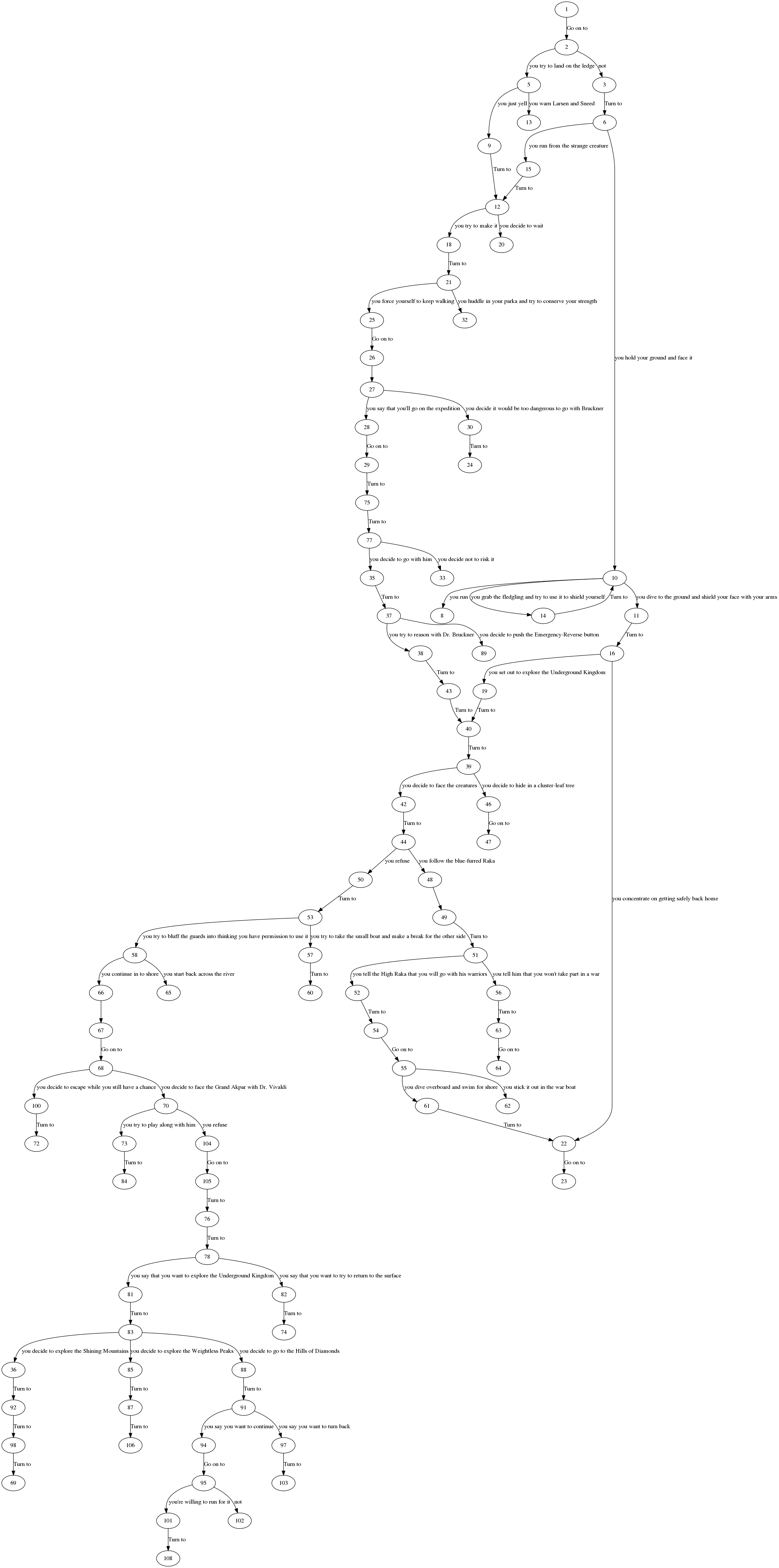
Choose your own adventure - 19 - Underground Kingdom

CYOA-19 is very similar to CYOA-18, although I think it's somewhat of an improvement. Instead of the almost linear story of CYOA-18, it has more choices at the start, creating a wider tree.

Still it very much represents a tree rather than a graph. The reasoning for this is probably so that there is an element of uniqueness and re-playability to it. As recombining branches usually means that there might as well have been one path to that point.

Still CYOA-19 has one loop, in one of the starting choices. It is 8 edges long, so not too bad. Interesting to note, without that loop it would have been a valid tree structure.

Conclusion

One thing I didn't expect to see as much when I started was loops, in fact the first implementation of the graph-viz script had no support for them.

It's also interesting to see the type of graphs develop over time, from something very complex to a simpler tree(-ish) structure.

In the end this is just a passing interest, and me sharing my work. I might add more books as I get my hands on them.

Interested?

If you're interested in this project or want more information, feel free to contact us! We are more than happy to help.