Diving into Evolutionary Strategies

In a recent project I've had the chance to work with 'self-learning agents'. While an easy way to go is to just take a common A3C library and use that, I wanted to explore evolutionary strategies (ES). They piqued my interest because of simplicity, and the recent paper by OpenAI on the topic.

In this article I'll explore evolutionary strategies and why they are more easily scalable than other reinforcement techniques.

Neuroevolution

At the base of ES is neuroevolution, a term used to describe all methods that creates a trained neural network from evolution. This can mean adjusting weights, architecture and/or biases.

Evolution is generally achieved by comparing slightly adjusted models, and comparing them; create a new generation from the best and start over. In a similar way biological evolution works.

In a more mathimatical sense, stochastic exploring of the reward gradient; i.e. a hill-climbing algorithm.

Evolutionary Strategies

Evolutionary Strategies (ES) is one of the simplest neuroevolution algorithm there is:

1. Create a master model with 'untrained' weights
2. From master, create population with randomly adjusted weights
3. Evaluate population in identical enviroments
4. Adjust master based on the the rewards
5. Go to step 2

See a minimal implementation here

Alternatively the entire algorithm can be described using the following formula:

$$m^{n} = m^{n-1} + L * \sum_{i=0}^{pop} E(m^{n-1} + J_i) * J_i$$
Where E is the evaluation function, J is an deterministic noise, and m is the model at a certain timestep, and L is the learning rate.
Although most implementations multiply a scalar (sigma) with J in order to get a smoother gradient.

While there are many different variants of ES, however most of them reach the same issues as most deep learning techniques: scalability. If you want to train a neural network, all executors need to be aware of the same changes in order to have meaningful optimization.

Distributed Training

The key to getting scalable training is randomness. While this may seem counter intuitive (if you're not familiar), randomness is actually our greatest advantage. Random Number Generators (RNG), can be created from a single number or seed while giving vastly different, but reproducible, results.

For regularly trained neural networks transmitting the entire model worth of weights to a nearby machine can take minutes. This is why Nvidia and similar companies have spent a lot of R&D on high-throughput links between GPUs.

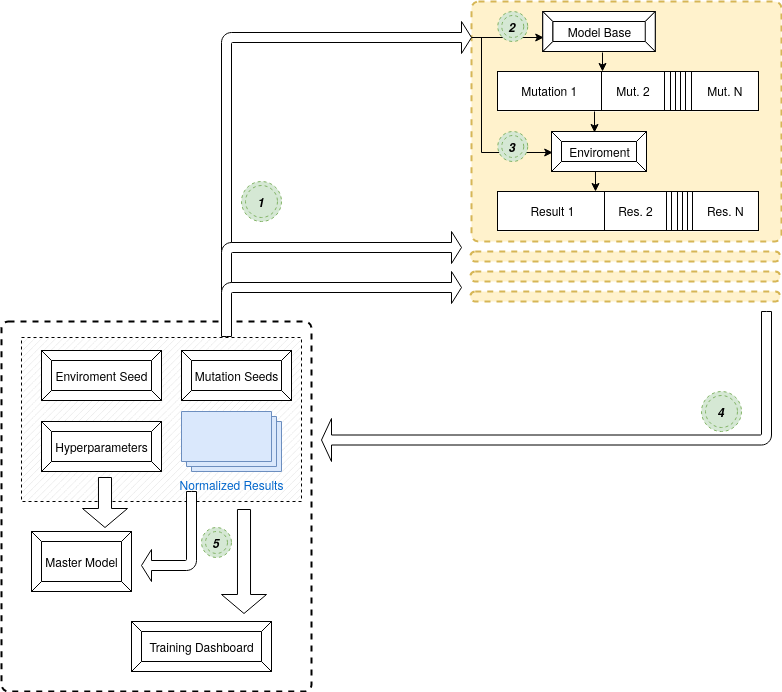
However with ES we can take advantage of the fact that all of the updates in ES are done from an RNG; the population is created by adjusting with RNG, then the master model is updated according to the population.

With that all we need to send over the wire to make it scalable is the seeds which corresponding to a certain agent in the population. Ideally the environment is deterministic so all the agents have a 'score' for the same test, but given a long/difficult enough task this wouldn't be a requirement.

Here is the flow from a birds eye view:

Results

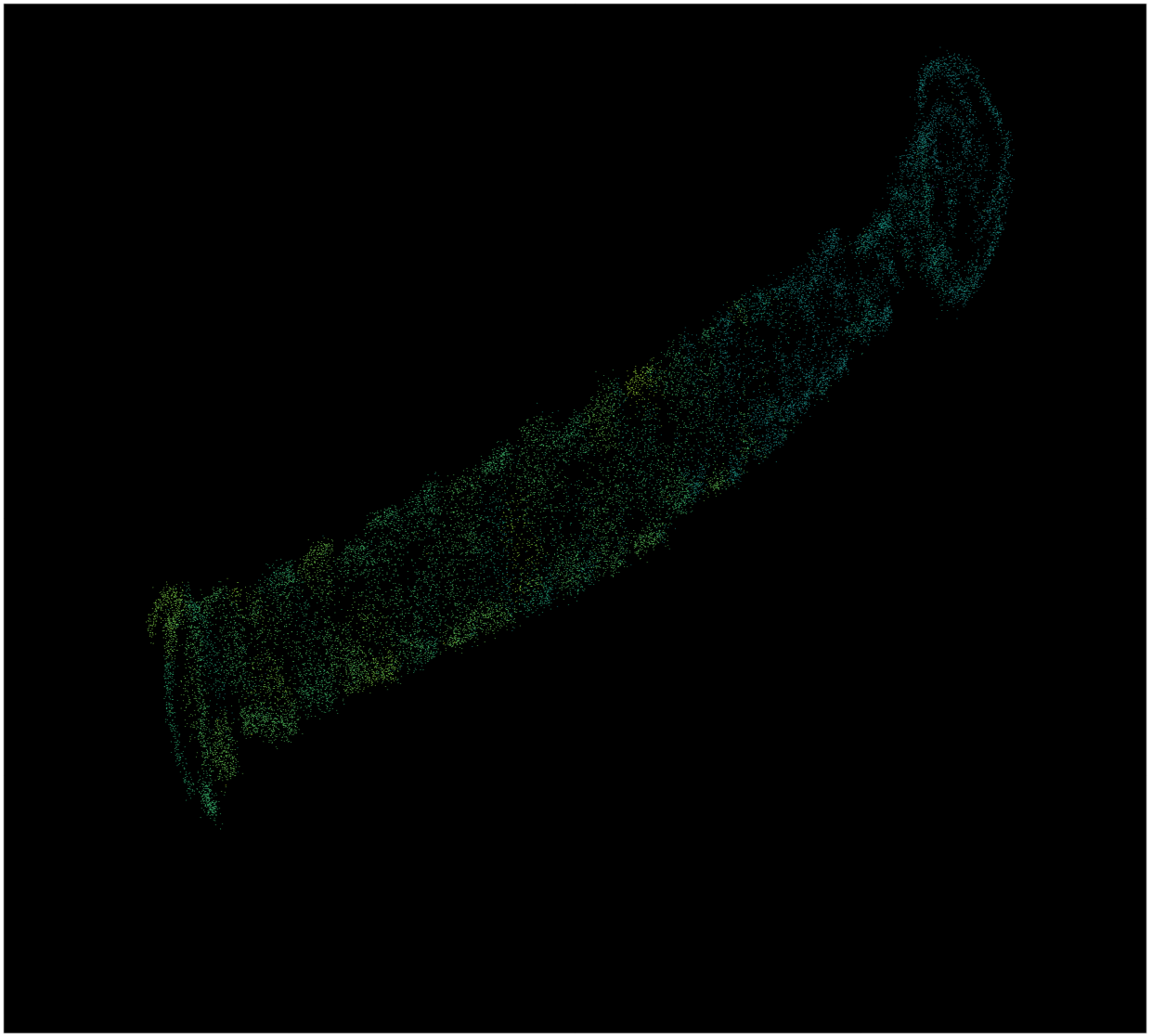
Below is a UMAP plot of all the different models in one training session (at a slow learning rate to get a nicer plot). The plot can be seen as the loss gradient for all of the parameters, reduced to a 2D image.

In the first part (top right), the model is exploring because this particular dataset requires some actions to be performed before any real change in reward is given. Afterwards the model goes slowly moving towards the higher rewards (bottom left). In total 21504 different models are shown each model having 19263 trainable parameters.